小学5年生の算数がとっても大事です!算数が好きなると、
学校へ行くことも楽しくなる。
これは不思議なんですが、うちの子は、そうでした。
今では、算数が一番好き!って言っています。
算数が解ける喜びを知ったみたいです。
大袈裟だと思いますよね?いいえ、事実です。なんだか毎日楽しく解いています。
※ここで言う算数は、計算問題ではなくて文章問題です。
算数好きはメリットしかないですよ~♪
- 算数ができるだけで、他の教科も出来るようになる。
- 小学校高学年になると、算数が苦手な子も多くなってくるので、
少しでも出来るようになると、自信につながる。 - 自信がついてくると、他の教科も学習したい!という欲が湧いてくる。
- 文章問題を解くだけで、国語力も付く!
問題の作者の意図していることを読み解く力を養える。 - もっと、もっとと、向上心が顕著に表れてくる。
試しにやってみてください♪
問題①
ある小学校の全児童は300人です。そのうち朝食にパンを食べる人は、学校全体の人数の30%です。朝食に白米を食べる人は、学校全体の60%です。そのほかの人は、朝食抜きの人です。
⑴朝食にパンを食べる人は、何人でしょうか?
⑵朝食抜きの人は、学校全体の何%になりますか?また何人ですか?
⑶朝食を食べる人と朝食抜きの人の人数の差は、学校全体の何%になりますか?
答え
⑴全児童300人のうち朝食にパンを食べる人は、30%であるので、
300×0.3=90
A.90人
⑵朝食抜きの人は、全体から30%と60%を引けばいいので、
100-(30+60)=10%となるので、
300×0.1=30
A.10%、30人
⑶朝食を食べる人は90%、朝食抜きの人は10%なので、
90-10=80
A.80%
問題②
お茶14.5dLを1.3dLずつ紙コップに分けると、1.3dLの紙コップはいくつできて、何dLあまりますか?
答え
14.5÷1.3をします。割り切れないです。ひっ算で、どれだけ余るか計算してみます。
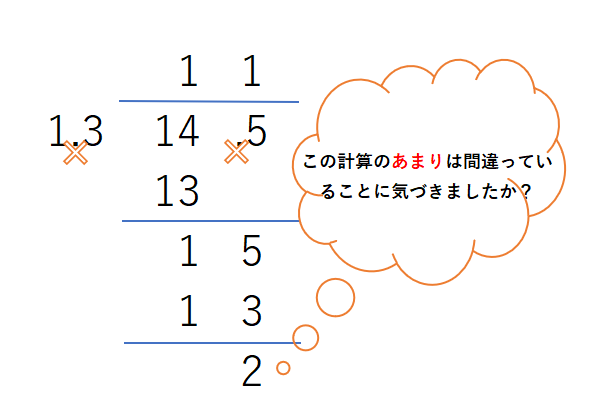
11と2余る…?これは間違いです。あまりについては、小数点を元に戻すことになりますので、0.2となります。
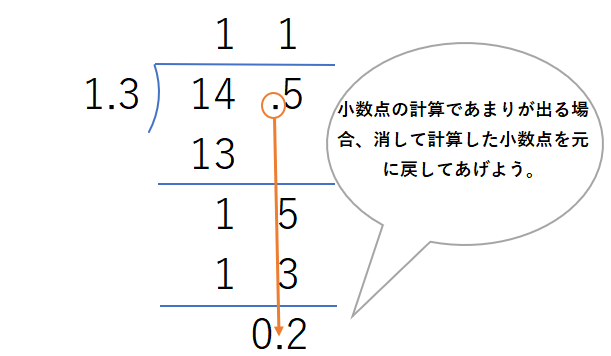
この問題は、難しいものではないのですが、計算方法を忘れてしまっている場合が多いので、注意が必要です!
ということで、答えは…
A.11個の紙コップができて、0.2dLあまる。
問題③
秒速2mで行進している人の行列があります。
人の行列の長さは60mです。この行列が、長さ200mのトンネルを通過するのに何秒かかりますか?
答え
イメージはこんな感じです↓

最後の人がトンネルを出るまでが道のりであるので、道のりは、200m+60m=260m。
時間は、道のり÷速さなので、260÷2=130
A.130秒
問題④
⑴秒速1mは分速何mですか?また、時速何㎞ですか?
⑵時速54㎞は分速何㎞ですか?また秒速何mですか?
答え
⑴秒速を分速に直すということは、1秒で1m進む場合、1分なら何mになるのか?ということ。
1分=60秒ですね。1秒で1m進むので、1分では60m走れることになります。
A.分速60m
また、秒速を時速に直すには、1時間でどれだけ走るか考えます。
1時間は60分、60分は3600秒であるので、1時間=3600秒となります。1秒で1m進むので、
3600秒(1時間)では3600m進むことになります。
=時速3600m
問題は、時速何㎞?となっているので、mを㎞に直します。1㎞=1000mであるので、
3600÷1000=3.6
A.時速3.6㎞
⑵時速を分速に直すには、⑴と逆の計算をすればよいです。
1時間で54㎞進むものが、1分ならどれだけ進むのかということです。
1時間=60分なので、54を60で割ってあげると1分で進む距離が出ます。
54÷60=0.9
1分だと、0.9㎞すすむことになります。
A.分速0.9㎞
また秒速を求めるには、1時間=60分=3600秒であることから、54を3600で割ります。
54÷3600=0015
よって、秒速0.015㎞
問題では、秒速何mかと聞いているので、
0.015×1000=15
A.秒速15m
問題⑤
ココちゃんが、家を出てから14分たったとき、ラムちゃんが自転車でココちゃんの後を追いかけました。ココちゃんの速さは分速60m、ラムちゃんの速さは分速200mです。
ラムちゃんは、何分後にココちゃんに追いつきますか?
答え
ココちゃんは、14分後には何m先に行っているか計算しましょう。
道のり=速さ×時間なので、
60×14=840
ココちゃんは、840m先に行っています。
そこから、ラムちゃんは出発します。1分ごとにこんな感じです↓

1分ごとに、二人の距離が縮んでいくのが分かります。
1分で、60m進むココちゃんと、1分で200m進むラムちゃんの差なので、
200-60=140
140mずつ距離が縮んでいくのです。
最初に二人の距離の差は840mだったので、それを140mで割れば、何分で追いつくのかが分かりますね。
840÷140=6
A.6分後
問題⑥
3.8㎏の水に200gの食塩を溶かしました。この食塩水は、食塩が何%の食塩水といえますか?
答え
割合の求め方は、比べる量÷全体の量です。
食塩+水は、全体の量、
食塩は、比べる量、ですね。(←全体の量に対して比べたい量)
3.8㎏をgに直します。1㎏=1000gなので、3.8㎏=3800㎏。
200g(比べる量)÷{3800g(全体の量)+200g}=0.05
A.5%
問題⑦
750gの水に食塩を250g溶かした食塩水があります。これに10%の食塩水500gを混ぜました。
何%の食塩水になったでしょうか?
答え
10%の食塩水には何g食塩が溶けているか考えます。
500×0.1=50により、50g食塩が溶けています。
これらをすべて合わせて、割合を出します。
食塩水の全体量は、750g+250g+500g=1500g
食塩の量(比べる量)は、250g+50g=300g
割合は、300÷1500=0.2
よって、20%の食塩水の出来上がりです。
A.20%の食塩水
まとめ
同じようなチャレンジ問題↓がありますので、是非使ってやってみてください♪
5年生の算数できるかな?道のり・公約数・公倍数・単位量あたりの大きさ


















コメント