小学生で、一番大事な算数を習うのは、5年生です。ここが出来ていると、中学生になったときに数学が嫌いになる確率がグンっと減ります。
5年生の数学が大事なことは分かっていましたので、自分なりに問題を作って子供に出したところ、ことごとく惨敗!!これは危ないとこでした!できなかったところを、重点的に繰り返しすることにより、劇的に算数ができるようになったのです。
得意とか、不得意とかを感じる差なんて、小学生の算数までは、努力で何とかカバーできます!どうカバーしていくか、それは、5年生の算数をどれだけ理解したかだけといっても過言はありません。
5年生の算数の問題です。確認してみてください。
問題①公約数?公倍数?
鶏のから揚げ105、ウインナー30本、おにぎり45個があります。これらをできるだけ多くの人に同じ数ずつ分けてお弁当パックにしたいです。
⑴いくつお弁当パックができますか?
⑵お弁当パックの中身は、それぞれいくつずつにするとよいですか?
答え
⑴同じ数ずつ分けたいので、公約数で考えます。最大公約数にするとできるだけ多くの人に分けられます。105と30と45の最大公約数は、15ですので、15パックのお弁当を作ればよいです。
A.15個
⑵それぞれ15で割ればよいので、
105÷15=7
30÷15=2
45÷15=3
A.から揚げ7個、ウインナー2本、おにぎり3つ
問題②1分でどれだけ近づく?
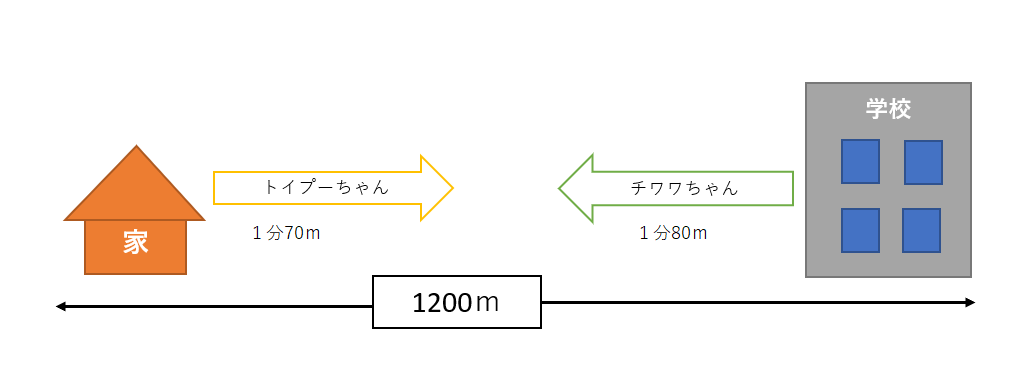
トイプーちゃんの家から学校までは1200mあります。トイプーちゃんは家から学校に向かって分速70mで、チワワちゃんは学校から家に向かって分速80mで、同時に出発しました。
二人は何分後に出会いますか?
答え
トイプーちゃんは、家から学校に1分で70mずつ、チワワちゃんは、学校から家に1分で80mずつそれぞれ進んでいます。
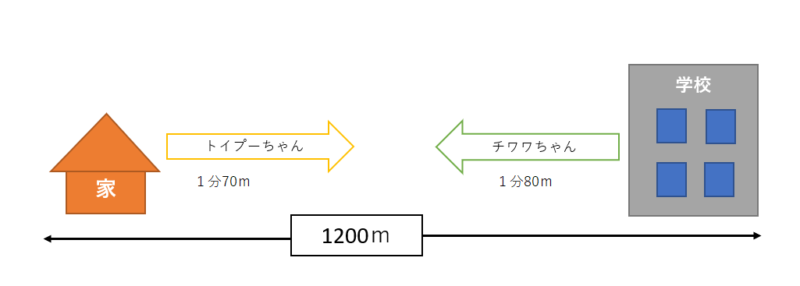
二人は、1分で150mずつ近づくことになります。これを表にします。

上の表を見ると、8分後には、二人は出会います。
二人が1分で150mずつ近づいていくので(70m+80m)、全体の距離1200mを150mで割れば、何分後に出会うか計算できることになりますね!式にしてみます。
1200÷150=8
A.8分後
問題③1分でどれだけ近づく?
ラムコちゃんが家を出てから14分たったとき、チイちゃんが、家から走ってラムコちゃんの後を追いかけました。ラムコちゃんの速さは、分速60m、チイちゃんの速さは分速200mです。チイちゃんは、何分後にラムコちゃんに追いつきますか?
答え
イメージはこんな感じです。↓
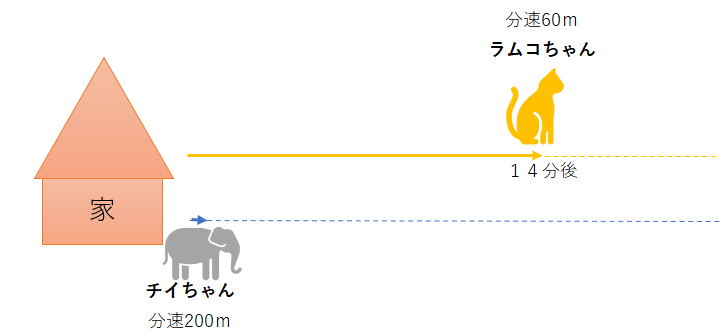
ラムコちゃんよりチイちゃんの方が速いスピードですね。1分で、二人の距離はどれだけ縮むのか考えます。表にしてみます。
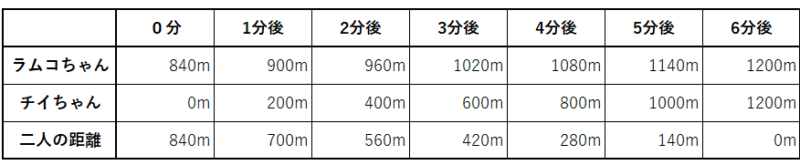
二人は1分で140mづつ距離が近づいていきます。(200m-60m)
ということは、最初に離れていた距離840mを140mで割れば、何分で追いつくか計算できます。
式にします。
840÷140=6
A.6分後
問題④公約数?公倍数?
ある学年では、男子36人と女子48人います。それぞれ同じ人数に分かれて、男女の混じったグループを作ります。余る人が出ないように、できるだけ多くのグループを作るためには、男女それぞれ何人ずつに分かれたらいいですか?
答え
それぞれ同じ人数で分かれて、グループを作るということは、公約数を使うといいですね。そして、できるだけ多くのグループを作るので、最大公約数が必要です。36と48の最大公約数は、12なので、12グループを作ることになります。
その場合、男子は、36÷12=3、女子は、48÷12=4
A.男子が3人ずつ、女子が4人ずつ
問題⑤単位量あたりの大きさ
2dLのペンキで、7㎡の壁に落書きします。
このペンキ13dLでは、何㎡の壁に落書きできますか?
答え
ペンキ1dLで、どれだけ落書きできるかというと、7㎡÷2dL=3.5㎡です。よって、13dLのペンキがあれば、13dL×3.5㎡=45.5㎡
A.45.5㎡
問題⑥倍数
1から100までの整数のうち、7の倍数はいくつありますか?
答え
7の倍数がいくつある?=7のかたまりがいくつある?ということです。ですので、100の中に7のかたまりがいくつあるのか調べます。
100÷7=14.28…となりますので、14個のかたまりががあることになります。
A.14個
問題⑦公約数?公倍数?
たて6㎝、横10㎝の長方形のカードを、同じ向きにすきまなくならべて、できるだけ小さい正方形を作ります。
⑴正方形の一辺の長さは、何㎝になりますか?
⑵たて6㎝、横10㎝の長方形は、何枚必要ですか?
答え
イメージはこんな感じです。↓
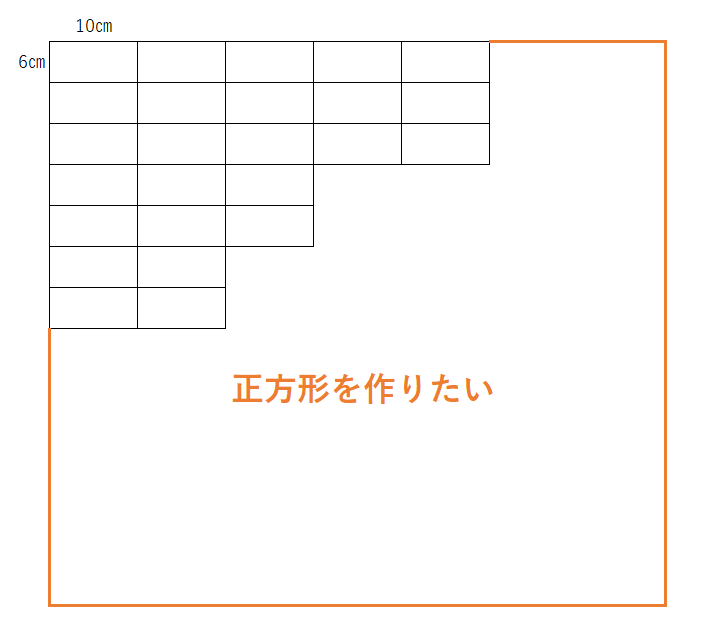
⑴出来るだけ小さい正方形を作るということは、6と10の最小公倍数を考えます。
6と10の最小公倍数は、60になるので、縦横60㎝の正方形を作ることになります。
A.60㎝
⑵60㎝÷6㎝=10、60㎝÷10㎝=6,となり、10×6=60枚必要になります。
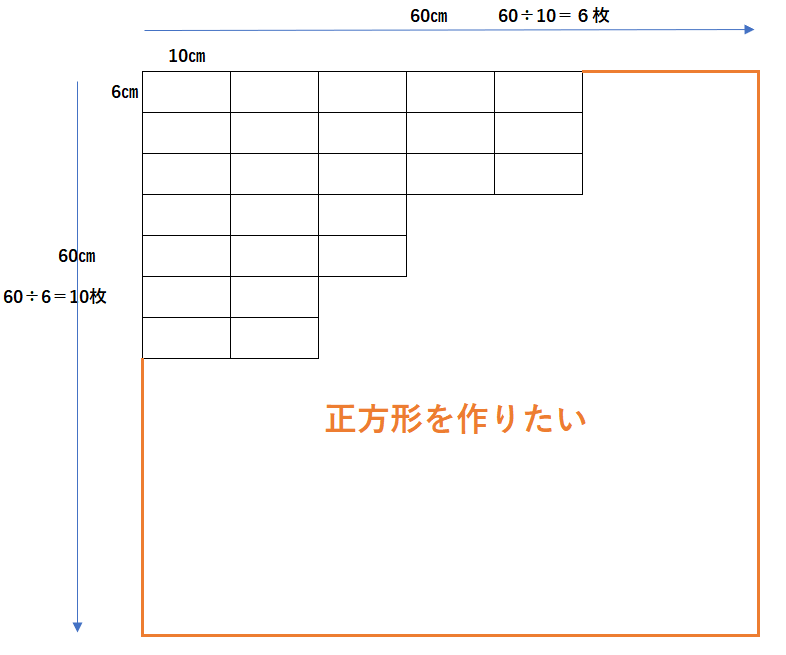
A.60枚
問題⑧公約数?公倍数?
たて14㎝、横21㎝の方眼用紙があります。
これを紙の余りが出ないように同じ大きさの正方形に分けます。できるだけ大きな正方形に分けるには、一辺を何㎝にすればよいですか?
答え
イメージはこんな感じです。↓
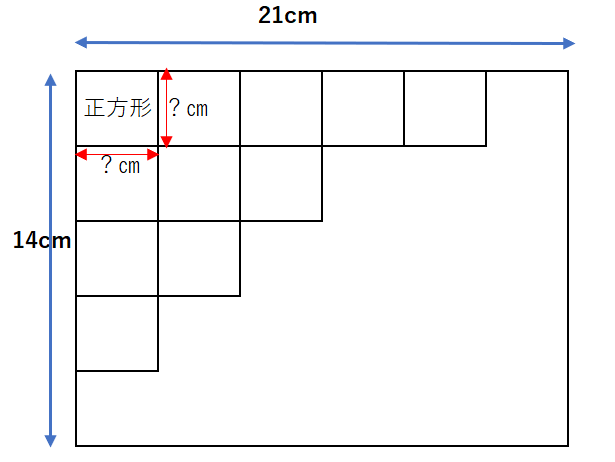
一枚の長方形の中に小さい正方形を敷きつめていくというイメージです。縦横同じ長さである正方形を入れていくので、一枚の長方形の縦横の長さの公約数を求めます。
14㎝と21㎝の公約数の中でも、最大公約数が必要になります(できるだけ大きな正方形)。14と21の最大公約数は、7になります。7㎝の正方形を敷きつめることになりますね。
A.7㎝
問題⑨道のり・時間・速さ
家から駅までの道のり2.1kmを、ラムコちゃんとチイちゃんが歩きます。
ラムコちゃんは分速70m、チイちゃんは分速75mで同時に出発しました。
⑴ラムコちゃんは家から駅まで何分かかりますか?
⑵また、チイちゃんとラムコちゃんのどちらが何分早く駅に着きますか?
答え
⑴時間=道のり÷速さですね。
しかし㎞とmで単位が違うので、まずはこれを合わせます。道のりを㎞をmに直すと、2100m。
ラムコちゃんの速さは、分速70mであるので、時間を出すには、2100÷70=30となります。
A.30分
⑵上と同じように、チイちゃんの時間を出します。
2100÷75=28となります。28分かかります。30-28=2となり、チイちゃんの方がラムコちゃんより2分早く駅に着きます。
A.チイちゃんが2分早く駅に着く




















コメント